为纪念我师赵松庭先生的《横笛的频率计算与应用》①发表四十周年，谨撰写此文怀念先师，并求教于同道，以期横笛频率计算在笛类乐器制作及其演奏中得到更广泛应用。

我自1973年起就用频率计算来制作笛子，1976年8月24日初步找出适应笛子实际温度的制作方法，并重新编制频率计算数据表（可以查找计算结果的表），1977年12月19日开始以适应笛子实际温度的频率计算方法制作笛子，迄今为止几乎所有笛子都用频率计算来制作的，并且每支笛子都留存数据档案，同时还记录一些问题和经验，这样做的目的是为了研究笛子，以便从中找出规律来。赵先生在1980年9月15日给我的信中说：“你是我的学生中首先掌握频率计算方法的一个，……我希望你再进一步完善计算的步骤，以及应用的方法。”为了不辜负老师的期望，我为此倾注了大量精力，在实践中不断检验理论。现将应用频率计算制作笛子的一些心得和问题探讨分述如下。

一、测量

由于笛子材料大多为天然生长的竹子，每支笛材的内径和管壁厚度都不相同，所以在选择合适的材料后要进行精密测量，要测出每个开孔位置的内径和管壁厚度，并设计好吹孔和音孔的大小，以及笛尾辅助音孔的位置。测量的准确与否，直接影响到笛子的质量，这是应用频率计算制作笛子须注意的一个问题。

二、计算

赵先生的《横笛的频率计算与应用》十分满意地给出了笛类乐器的频率计算方法，但还有一些问题尚需进一步探索和研究，在解决频率计算方法后，温度的问题就成为研探的焦点，正如赵先生在文中指出的“管内平均温度，尚需另加一个修正数。”“实际温度以气温为准。在乐器制造上需要另外寻求适应实际温度的方法，需要有专题探讨。”“我们的探讨还有些不完善之处（估计还有2%的误差）。"这些正是需要为之解决的问题，将横笛频率计算进行到底那是迟早的事。

在掌握频率计算方法后，温度对笛子频率的影响就成为制作的关键，这关系到制成的笛子适合于什么气温时吹奏的问题。若以气温标准有效管长计算的笛子，一般情况下制成的笛子会比标准频率高，这是因为笛管内的温度比实际气温高的缘故。例如以5℃有效管长制成的笛子在5℃时吹奏，笛子的频率将比标准频率高32音分左右，实际上它适合于-10.5℃时演奏；以15℃有效管长制成的笛子在15℃时吹奏，笛子的频率将比标准频率高21音分左右，实际上它适合于4.5℃时演奏；以25℃有效管长制成的笛子在25℃时吹奏，笛子的频率将比标准频率高11音分左右，实际上它适合于19.5℃时演奏等。这样，对于演奏者选用笛子带来了麻烦，所以我们在标明笛子温度标准时，应以实际气温为准，比如15℃标准的笛子就应适合在气温15℃时演奏符合标准频率等。同时，从以上例子中看到管内平均温度对频率的影响很大，因此在频率计算和实际应用中决不能忽视。

下面我们来探讨适应实际温度的方法。我们能否寻找一种有效管长来计算制作笛子，并使之在指定气温下符合标准频率？比如要制作15℃标准的笛子，应选用的有效管长是多少？如果能够找到，我们可以同样的方法找到所有能适应实际气温的有效管长，也就找到了适应实际温度的方法，同时也解决了管内平均温度的修正数问题。下面通过计算来求证一个规律。

分析：因为以15℃有效管长制作的笛子在15℃时吹奏，大约高于标准频率21音分，因此在计算时把给定频率降低21音分，算出有效管长，再以此有效管长计算制笛，其结果必然能得到15℃标准的笛子。

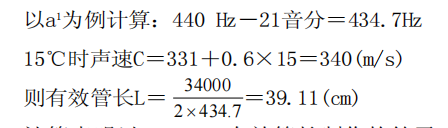
计算表明以39.1lcm有效管长制作的笛子，假设吹入笛管内的气流温度为15℃，则a1的频率为434.7 Hz，然而笛子是给人吹的，在15℃时吹奏，管内平均温度为22℃，上升了7℃，笛子将升高21音分，那么频率正好补足为440Hz，符合标准频率。因此，这39.11cm有效管长就是我们要寻找的有效管长，它是适应实际温度15℃时al的有效管长。再看这39.1lcm有效管长所对应的声速和温度是多少呢？

先求出声速：C=2LF=2×39.11×440=344.17(m/s)

说明此时的大气声速为340m/s，而管内声速为344.17m/s。为什么认定344.17m/s是管内声速呢？因为我们没有力量来改变15℃大气的声速。

然后根据声速公式C=331＋0.6θ℃算出管内声速之温度：

θ=（C-331）÷0.6=（344.17-331）÷0.6=21.95（℃），正好是气温15℃时的管内平均温度，这样我们就找到了适应气温15℃的有效管长为22℃有效管长。这一事实反映了事物本身不以人的意志为转移的客观规律，影响笛箫频率的最终温度是“天人合一”的管内温度，管内声速是影响频率的直接原因，取与气温相对应的管内平均温度有效管长来计算，是适应实际气温的必然方法，也是应用频率计算制作笛子最简捷的路径。

那么声波从一种温度传播到另一种温度的空气中时将有什么变化呢？从笛子发声的声学特征看，振源在笛管内，其声波传播到与管内不同温度的大气中，波长与声速成正比变化，振幅随声波能量的逐渐减弱而缩小，而频率是不会改变的。至于火车向你驶来，音调变高，火车驶离你远去时，音调变低，这种由于波源和观察者之间有相对运动，使观察者感到频率发生变化的现象，在声学上叫做多普勒效应。这是我们在研究声速和频率关系时，必须区分的两种不同性质的物理现象。

接下来是管内平均温度的确认，因为上述求证的根据是管内平均温度。赵先生的管内平均温度公式θ=1/3（36-t）＋t（θ为管内平均温度，t为气温，36 为人的体温），可以根据气温求得管内平均温度。虽然笔者在管内平均温度测验中测得的平均温度比赵先生的略高了一点，但我觉得赵先生定的平均温度处于“弹性位置”，正如吹笛子用气不爆不虚，以我长期的制作实践经验，觉得这个公式是符合客观实际的，是可行的。实践证明取管内平均温度有效管长计算制成的笛子，在与其相对应的实际气温下吹奏是符合标准频率的。

三、音孔定位

用频率计算求得的各音孔位置，并不适合于所有笛子，大笛和低音笛可以直接用计算所得的数据来确定音孔位置，但梆笛（就六孔笛来说）主要是第二和第三音孔之间的距离过近，手指无法按孔，因此，须将第二音孔放大下移，第三音孔缩小上移。曲笛的第二、三孔也要作适当调整，手指按孔才舒服。上移或下移多少也可通过计算求得。例如有一支G调梆笛计算所得吹孔至各音孔的距离如下（单位：cm）：

这时我们看到第二音孔至第三音孔的距离为18.27-17.35=0.92（cm），因为孔距是从孔中心算起的，计算时设计的音孔平均半径为0.4cm，在笛子上开成椭圆形的孔，横半径与竖半径分别为0.35cm与0.45cm，那么两音孔的半径合起来已达0.9cm，说明第二第三音孔已相连，因此必须将这两个音孔拉开距离，并使手指能比较舒服的按孔。现将第二第三音孔移位计算如下：（单位：cm）

1.吹孔至第三音孔的距离（将第三音孔半径缩小为0.35cm）：

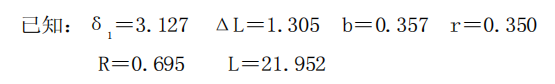
2.吹孔至第二音孔的距离（将第二音孔半径放大为0.45cm):

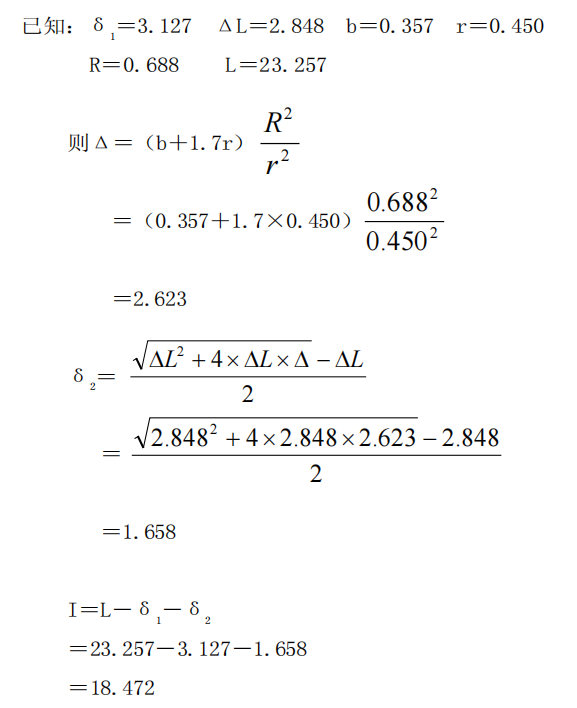
经过以上计算可知第二第三音孔之间的距离已调整为:

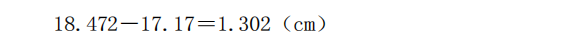
若减去两个音孔的半径，则两音孔边缘还间隔0.4cm，使手指能比较舒服的按上音孔，并保证了音孔移位后的音准。

因此，对频率计算后的数据视情况作准确合理的调整，是应用频率计算制作笛子须注意的又一个问题。

另外，对于第六音孔，可根据演奏者需要作适当调整，以全按作2为例，若要用按四、五孔开一、二、三、六孔的指法吹1，则第六孔在开孔时要作适当变化。

四、校音

正因为人吹笛子时的气流温度对笛子频率有很大影响，所以在校音前须吹一会儿笛子，使笛管内温度达到相对稳定。这是笛子校音或检测时须注意的问题。

笛子的校音有两种情况：一是制作室温度与笛子的温度标准相同，这时只要使用音频仪直接校音，音分调整数为±0；二是制作室温度与笛子的温度标准不一致，在笛子制作中多数是这种情况。那么，在校音时要算出温差与音分差，所谓温差在这里是指制作室温度与笛子的温度标准的差，音分差是温差的2倍，即温差每1℃±2音分，制作室温度高于笛子温度标准的音分读数增加，反之则减少。至于为什么温差1℃要士2音分而不是士3音分呢？我们可以通过频率计算来求证。虽然用频率公式计算温度与频率的变化关系是温度每±1℃频率±3音分，但由于气温的升降与管内平均温度的升降，两者不是等量变化，且两者又是因果关系，所以我们首先要弄清制作室温度与笛管内温度的相互关系，通过管内平均温度算式可以算出制作室温度（气温）每升高1℃，笛管内平均温度升高多少？

通过计算得出的结论是：气温每±1℃，管内平均温度士0.667℃.而对笛子的频率直接起作用的温度是笛管内温度，所以我们只要通过公式来计算出笛管内每 0.667℃的频率变化数，也就知道了制作室温度每1℃的音分差数。

根据同一支笛子在两个不同温度时的频率比公式：

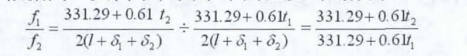
式中l为实际管长， 为为吹孔校正量，为末端校正量。

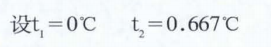
则笛子在两个不同温度时的音分差数为：

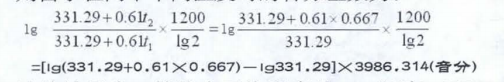
计算结果为：笛管内平均温度从0℃升至0.667℃时，频率升高2.12音分；而温度由36℃升至36.667℃时，频率升高1.99音分。因此可以说气温每±1℃，笛子频率相应±2音分。这个结论直截了当的道出了气温与笛箫频率的变化关系，不走弯路，方便利用。所以，不管是否应用频率计算来制作笛子，都要进行校音，在校音时按照温差每1℃±2音分来计算音差，是校音时必须掌握的一个问题。

举例一：在气温25℃时要制作15℃标准的笛子，音差是几音分？

分析：这个问题实际上也就是15℃标准的笛子在气温25℃时吹奏，音差是多少？同时要明确15℃标准的笛子是用22℃有效管长计算制作的，如以15℃有效管长计算制作的笛子，就比标准频率高21音分，也就不能称为15℃标准的笛子，所以概念必须要清楚。

计算：（25-15）×2=20（音分）

计算结果表明在校音时调整到音频仪读数为＋20音分，就这么简单。另外，因为作用于笛子的最终温度是不同气温下的不同管内温度，所以上例也可以通过管内平均温度来计算：15℃时的管内平均温度为22℃，此时吹奏频率符合标准频率，即音频仪读数为±0，在25℃时的管内平均温度应为28.67℃，那么（28.67-22）×3=20（音分），但在计算上走了一点弯路，不大众化，不方便利用。

但若把它算成（25-15）×3＋（28.67-25）×3 =41（音分）那就错了。为什么要举这个例子？因为“气温每±1℃笛箫频率±3音分”已在笛界广泛流传，在应用上造成了误导。这个算法初看很有道理，因为气温相差10℃频率上升30音分，再加上在25℃时吹奏，管内平均温度上升到28.67℃，上升了3.67℃，计11音分，合起来就是41音分。能看出这种计算方法错在哪里吗？错在对温度标准的概念不清，要知道这

15℃标准笛子是用22℃有效管长制成的，要不就比标准频率高21音分，把41音分减去高于标准的21音分，结果还是20音分，仍然是气温每±1℃笛箫频率士2音分。当然，我们也可用频率计算来证明上述“41音分”的错误，不再赘述。

要指出的是赵先生在对温度的论述中，是把气温和管内平均温度分开来探讨的。在论述气温时的频率计算中没有联系人吹奏的实际情况，所以这个温度率只能适合吹入笛子的气流与大气温度相同时的条件；在论述管内温度对频率影响时，说明了管内温度变化对频率影响很大，管内平均温度尚需另加一个修正数。笔者认为赵先生是清楚这些问题的，所以他要我们去进一步完善计算的步骤和应用的方法。气温和管内平均温度是事物的两个方面，我们不能片面地理解和机械地应用它，应该把它们联系起来看，才是全面看问题的辩证的方法。

举例二：在8℃环境下要制作温度标准为25℃的笛子，a'的有效管长是多少？校音时音频仪上的读数（音差）多少（音分）？

计算：

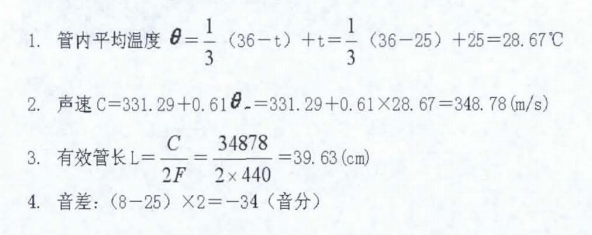
因此，不管在何种气温环境下，通过频率计算都可以有把握地制作出预期要适应的温度标准的笛子。

另外须注意的是笛膜对频率也有影响，包括笛膜的厚薄以及松紧，厚、紧音高，薄、松音低，美纹纸比芦苇膜大约高10音分左右，这也是校音时应该注意的。

综上所述，我们在用频率计算制作笛子时，必须读懂赵松庭先生的《横笛的频率计算与应用》一文，充分理解其计算原理和温度对管乐器频率的影响之内涵，才能使计算和应用更加完善。希望大家共同来探讨和实验，理论如经不起实践的检验，那必然是错误。本文如有不当之处，欢迎同道不吝指教。

注：①见《乐器科技简讯》1973年第二期。