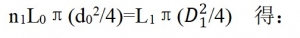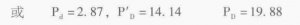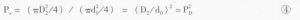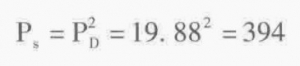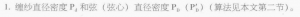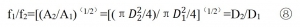一、概述

古琴的七根弦在琴面上的长度相同，为了要求各弦散声频率(高低)不同，那么各弦的直径(粗细)和张力(松紧)就应该有所差别。为了演奏方便和其他原因，一般要求各弦的张力接近平衡，因此各弦的直径之间要有一定的比例关系。

最细的一根弦(第七弦)的粗细及松紧程度到底如何？要从按弹方便和材料强度等方面来考虑。第七弦直径一经决定，其他各弦的直径也就可以决定了。至于“缠弦”则另以缠纱缠在“弦心”上，这一方面增大了弦的直径，另一方面也起了美化音色的作用。缠纱也有一定要求，太粗就不光滑，摩擦力大，弹时有噪音，太细又易磨损，此外还应考虑加工方法、胶合材料等。因此制弦时就要全面考虑，并作一系列试验，才能求得最好的参数(例如弦截面直径大小、用丝量、缠纱粗细、搓合后缩短率、用胶量等)。但是其中有一点是必须首先要做到的，那就是各弦直径大小要有一个概略的算法，以便制弦时有所依据，同时也可以将历代琴弦的粗细大约计算出来，考察其演变过程，以便吸取前人的有益经验。

制弦方法从古以来一般是以若干茧作一“单位”(例如茎、丝、纶等)，再以若干“单位”“搓”成四股“合”为弦心。各弦的“单位”数视其粗细不同而异。古时缠弦三根(一、二、三弦)，近代则为四根(一、二、三、四弦)。另以若干“单位”搓成缠纱缠在弦心上。非缠弦，则弦心就是弦的本身。由于搓合及缠上缠纱，弦直径增大，增大多少要加以计算。

由于古代的“单位”(茎、丝、纶等)的粗细到底怎样尚不很清楚，因此只能求出其相对值(密度)，也就是求出某弦直径能折合多少个“单位直径”(即茎、丝、纶的截面直径)。此外，为了便于研究起见，另以每一组弦(一至七弦)中的最细一根弦(第七弦)的直径长度定为百分之百(100%)，再求出其他弦对第七弦的百分比，这样如果能够知道其中任意一根弦的直径实际值，便可推出其他诸弦的直径实际值了。近来苏州方裕庭所制的第七弦直径0.77mm，张在以第五弦为大字组A(频率=110Hz)调成正调的琴上，即该第七弦之频率=110(4/3)≈146.67时，按弹也颇方便。因此姑且假定历代大琴弦的第七弦直径都以长0.77mm来计算，以求出其他诸弦直径的长度值以做参考。假如能得到全部必要资料，可以再算出历代各式琴弦直径的实际值。

由于资料不全，并忽略一些次要因素，有的参数和条件只能假定，又没有实验证明，所以只是概略的计算，其中有本文作者主观意见，可能有错误之处，仅供古琴研究和制弦者的参考。

二、概算公式的推导

我们可先假定每“单位”(茎、丝、纶等)的直径长度为已知量，以求出：

1.弦之直径密度PD(弦直径长度/单位直径长度)，即弦直径所折合的“单位直径”数。

2.弦心之直径密度P’D(弦心直径长度/单位直径长度)。

3.缠纱之直径密度Pd(缠纱直径长度/单位直径长度)。

现在令

拉紧而未搓合前每“单位”直径长度为 d0(已知)

若干“单位”搓合后所成弦心直径长度为 D1

若干“单位”搓合后所成缠纱直径长度为 d1

弦(弦心加上缠纱后)总直径长度为 D2(非缠弦之D1=D2)

每根弦心之总单位数为 n1

每根缠纱之单位数为 n2

弦心搓合后之缩短率为 K1%

缠纱搓合后之缩短率为 K2%

K1% = 搓合后弦心长度/搓合前弦心长度  100%

K2% = 搓合后缠纱长度/搓前缠纱长度 100%

现忽略一些次要因素假定：

1.拉紧时各“单位”(茎、丝、纶)之直径长度相等为d0。

2.搓合后之弦心、缠纱和弦之截面皆为标准圆形。

3.搓合前后总体积不变(即不考虑弹性变形)。

4.胶不占体积。

根据以上假定，便可用纯几何方法简单地推出概算公式。

现在再设未搓前拉紧之一束“单位”丝均长为L0。

搓合后成为弦(弦心)之长为 L1(L1<L0)

则K1% =L1/L0  100%。

由于“单位”、丝和弦都是圆柱体，所以

V=Lπr2=Lπ(D2/4)公式中

V 为圆柱体体积

π 为圆周率3.1416

r 为截面半径

D 为截面直径

因此搓合前每“单位”体积为

V0=L0π(d02/4)

n1个“单位”体积构成搓合前总体积为

Vo=n1v0=n1L0π(d02/4)

同理，搓合后弦心总体积为

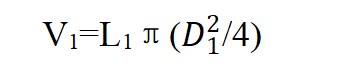
假定V0=V1，故

D1=[n1/(L1/L0)]（1/2）d0=(n1/K1)（1/2）d0 ①

同理可得缠纱直径d1=(n2/K2)（1/2）d0 ②

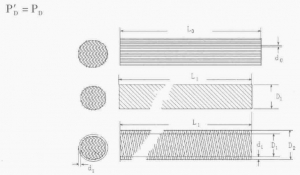
弦直径D2=D1+2d1(见图1) 即D2=[(n1/K1)（1/2）+2(n2/K2)（1/2）d0 ③

或Pd=d1/d0=(n2/K2)（1/2）②’

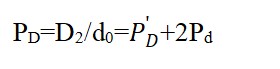
=(n1/K1)（1/2）+2(n2/K2)（1/2） ③’

非缠弦之

图1参数示意

以《谢希逸合弦法》第一弦为例(见表1)

知其“单位”为茎，n1=180  n2=8

K2% =97.5%  K1%=90%

d1=(n2/K2)（1/2）d0=(8/0.975)（1/2）d0=2.87d0

D1=(n1/K1)（1/2）d0=(180/0.9)（1/2）d0=14.14d0

D2=D1+2d1=14.14d0 +2×2.87d0 =19.88d0

若要知道该第一弦截面积相当多少个单位面积，则因面积A=π(D2/4)

所以面积密度为：

第一弦之面积密度

即相当于用394茎。

三、历代古琴直径(密度)概算一览表(表1)[1]

(一)数据部分

1.数据栏内材料是根据查阜西先生所收集制订的《历代古琴弦缠制合规格演变一览表》中抄得，其中《伯牙合弦法》、《唐陈拙合弦法》两项数据不全，不加推算。

2.有带括号()之数据系假定的。例如n2栏中之(8)、K1%栏中之(80)等。在原数据缺乏时，唐代之n2和K1%分别假定为8及80%，宋代则为7及75%。

3.K2%一律假定为97.5%(60尺缩短1.5尺)。

4.苏州方裕庭制弦数据是把它张在“以五弦为A调成正调”的琴上用千分尺测得结果(该弦系1956年卖与北京古琴研究会的)。

(二)计算部分

2.各弦相对百分比q%。

以第七弦直径D（7）为100%，求其他诸弦直径的百分比：

q%=(D/D（7）)100% ⑤

以“唐第一个又合弦法”为例：

第一弦直径：D（1）=18.94d0

第二弦直径：D（2）=18d0

第三弦直径：D（3）=16.9d0

第六弦直径：D（6）=10d0

第七弦直径：D（7）=8.65d0

所以，第一弦之相对百分比为q%（1）=(18.94/8.65)%=219%

同理，二、三、六诸弦之相对百分比q%分别为208%、196%、115.8%。

3.以大琴弦第七弦直径为0.77mm计时，其他各弦直径值D的计算(单位：0.01mm)。

(1)大琴弦计算

第七弦定为77，所以其他各弦直径为：

D=77q % ⑥

再以“唐第一个又合弦法”为例，则

D1=77  q（1）%=77×219%=169

即第一弦直径为169(0.01mm)。

同理，推得二、三、六诸弦直径为160.5、151、81.8(单位：0.01mm)。

谢希逸法第七弦无数据，所以令第五弦为0.93mm(与苏州方裕庭弦同值)，定为100%。

同理，推出同组中其他各弦直径长度值。

(2)中小琴弦计算

(甲)《太古遗音·造弦法》、《与古斋琴谱·造弦法》之大、中、小弦的“单位“一样(同为纶)，而所用纶数不同。

例如《太古遗音》大琴弦第七弦之D大=11.85d0

中琴弦第七弦之D中=11.55d0

小琴弦第七弦之D小=10.31d0

所以可求出

D中=(11.55/11.85)D大=(11.55/11.85)×77=75(0.01mm)

同理

D小=(10.31/11.85)D大=(10.31/11.85)×77=67(0.01mm)

《与古斋琴谱·造弦法》可同理推算出来。

(乙)《天闻阁琴谱·适弦法》

大、中、小三种琴弦的“单位”不同(纶[纶]{纶})。

大琴用纶 9丝为一纶

中琴用纶 7丝为一纶 故设其单位为 [纶]

小琴用纶 5丝为一纶 故设其单位为{纶}

前已证明二个圆面积之比等于二个圆直径平方之比，即

(A1/A2)=(D1/D2)2     (D1/D2)=(A1/A2) 1/2

三种纶所含丝数不同，意味着三种纶的截面积A不同，所以

(D中/D大)=(A中/A大)1/2

D中=D大(A中/A大)1/2=77×(7/9)1/2=68(0.01mm)

同理

D小=D大(A小/A大)1/2=77×(5/9)1/2=57.5(0.01mm)

中小琴弦第七弦直径已知，便可照大琴弦一样的算法推出一组弦中其他各弦直径值。

例如《天闻阁琴谱》中小琴弦第三弦的直径值：

D（3）=D（7）q%（3）=57.5×187%=107.5(0.01mm)

4.本表系用计算尺计算有效数字三位。

四、讨论

(一)按声学原理知紧张的弦振动发声时

f=(1/2L)(F/m)（1/2）=(1/2L)(F/A·p)（1/2）

其中：f是频率即每秒振动数；

L是弦的长度；

F是弦的张力；

m是单位长度弦的质量；

A是弦截面积；

p是单位截面积单位长度弦的质量。

所以两根弦频率之比为

：f1/f2=[(1/2L1)(F1/A1·p1)（1/2）]/[(1/2L2)(F2/A2·p2)（1/2）]

在琴上L1=L2   (琴面上各弦等长)

P1=P2   (假定各“单位”丝均匀，见前)

所以 f1/f2=[(A2/A1) (F1/F2)（1/2）⑦

若再假定张力相等，即F1=F2，则

即琴上各弦张力相等时，各弦频率与直径长度成反比。

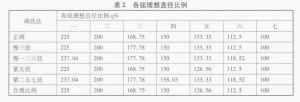
(二)根据公式⑧，可推出各弦直径长度之间的合理关系。古琴之调弦法最常用的有正调、慢三弦、慢一三六弦、紧五弦、紧二五七弦五种，现分别讨论如下

1.正调

因在同一弦上频率与长度成反比，而十徽在全弦3/4处，九徽在全弦2/3处，七徽在全弦1/2处。所以第十徽按音频率为散音之4/3倍，第九徽按音频率为散音之3/2倍，第七徽按音频率为散音之2倍。现求各弦散音频率与第七弦散音频率之比值。

设各弦频率分别为f1→f7，各弦理想直径分别为D1→D7，则

f5=(3/4)f7         (七弦散音与五弦十徽相应) 羽逆生角

f4=(2/3)f7         (七弦散音与四弦九徽相应) 商顺生羽

f6=(4/3)f4=(4/3)(2/3)f7

(六弦散音与四弦十徽相应) 徵逆生商

=(8/9)f7

f3=(2/3)f6=(2/3)(8/9)f7

(六弦散音与三弦九徽相应) 宫顺生徵

=(16/27)f7

f2=(1/2)f7

(七弦散音与二弦七徽相应) 二弦为羽音倍律

f1=(1/2)f6=(1/2)(8/9)f7

(六弦散音与一弦七徽相应)一弦为徵音倍律

=(4/9)f7

所以q1% =D1/D7=f7/f1=9/4       =225%     (第一弦)

q2%=D2/D7=f7/f2=2           =200%     (第二弦)

q3% =D3/D7=f7/f3=27/16   =168.75%  (第三弦)

q4% =D4/D7=f7/f4=3/2       =150%     (第四弦)

q5% =D5/D7=f7/f5=4/3       =133.33%  (第五弦)

q6% =D6/D7=f7/f6=9/8       =112.5%   (第六弦)

q7%               =100%     (第七弦)

2.慢三弦

3.慢一三六弦

4.紧五弦

5.紧二五七弦

f5=(3/4)f7         (七弦散音与五弦十徽相应)

f3=(3/4)f5=(9/16)f7  (五弦散音与三弦十徽相应)

f6=(3/2)f3=(27/32)f7    (六弦散音与三弦九徽相应)

f4=(3/4)f6=(81/128)f7  (六弦散音与四弦十徽相应)

f2=(1/2)f7          (七弦散音与二弦七徽相应)

f1=(1/2)f6=(27/64)f7 (六弦散音与一弦七徽相应)

所以

q1% =D1/D7=f7/f1=64/27=237.04%

q2%=D2/D7=f7/f2=2 =200%

q3% =D3/D7=f7/f3=16/9=177.78%

q4%=D4/D7=f7/f4=128/81=158.03%

q5% =D5/D7=f7/f5=4/3=133.33%

q6% =D6/D7=f7/f6=32/27=118.52%

q7% =100%

6.把以上数据列成表2

因为琴弦如过紧(超过原来规定值)，特别是较粗弦过紧时不易按弹，所以应以五种调弦法中各弦理想直径比例值最小的定为合理比例。又现时有的一些古琴弦与琴面距离由七弦至一弦次第增大，所以一弦至六弦之合理比例实际上应再减低一些，即各弦张力自七弦至一弦应次第减低一些。

(三)历代琴弦直径比较

观察表1，那么历代琴弦直径演变过程便一目了然。清以前的琴弦直径大体上还合理，其中似以“齐嵩论弦法”为最，该组弦调成正调，则只第一弦稍松一些，其第三弦之q%=178近似于调成正调时第三弦要求之q% (178.78)。清代之第三、四弦过粗不太合理。方裕庭的缠纱都细一些。

(四)对《与古斋》、《天闻阁》制弦法的意见

清以前各弦“单位”(茎、丝、纶)数多用递减(20、34等递减)，虽无理论根据，但基本上还合理，因为他们是从经验中得到的数据。到清代，《琴苑心传全编》之一至五弦(宫、商、角、徵、羽)诸弦纶数的关系是与“三分损益”相符，六、七弦例外。到《与古斋》、《天闻阁》则七弦纶数的关系(不计缠纱)全部按“三分损益”进行(按三弦为宫计算)，好像是有理论根据了。可是按声学原理如诸弦张力一样则各弦频率是与各弦纶数(相当于截面积)之平方根成反比，“三分损益律”是不能适合的。用“三分损益律”即意味着频率(古琴各音间是“三分损益”的关系)与截面积成反比。

例如第三弦与第六弦之频率比：

f3：f6=2：3(宫顺生徵，把琴弦调成正调时)

那么，第三弦与第六弦纶数n的比应为：

(n3)（1/2）：(n6)（1/2）=3:2，即

n3:n6=32:22=9:4

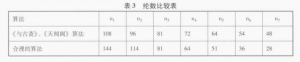
若以第三弦纶数n3=81，则

第六弦纶数n6=81(4/9)=36

第四弦纶数n4=(4/3)2n6=(16/9)×36=64

第七弦纶数n7=(2/3)2n4=(4/9)×64=28.444≈28

第五弦纶数n5=(4/3)2n7=(16/9)(4/9)×64=50.568≈51

第二弦纶数n2=22n7=113.776≈114

第一弦纶数n1=22n6=144

把数据列成表3，可见二者很不相同。

用“三分损益”推算纶数的理论本来已不合适，而缠弦是又加上缠纱的，这样《与古斋》和《天闻阁》又将他们持为根据的理论破坏，显得自相矛盾。本文作者很怀疑清代的琴弦是否按他们的理论制成。清代学者能从理论上探讨是一可喜现象，可是他们的理论本身有缺点而又脱离实际，未免有些“闭门造车”了。

五、其他意见

1.制弦时除对弦的直径有一定要求外，其他像胶合材科、弦之光滑程度、韧性……都应特别注意。如缠纱与弦心脱离，则缠弦之声音发哑。又我们的古琴弦在弹奏时有噪音(摩擦音)是一个缺点，最好能设法改进。

2.若能知道丝的实际粗细、韧度、合理的缠纱粗细等材料时，也可以从琴弦直径之要求，反过来推算出各弦应采用的单位数，现因材料不全故从略。

3.本文推算公式中的一些假定是忽略一些次要因素使得推导方便出发的。例如实际上缠纱因搓得松，缠上时成为扁形(非圆形)，实际有些出人，所以只是概算。至于本文所提的一些意见是否完全合理，还有待于实验的证明。

原载《传统的造弦法》一书附录，1957年

[1]表1在第326—327页之间。