内容提要: 文章列举了具有中国胡琴类弓弦乐器类型样本之典型意义的二胡、京胡和板胡,从其声音振动的物理模式视角出发,分析了这三种乐器声音特点所产生的物理原因,研究了乐器构造对其音色的影响,进而推论了不同乐器音色类型对人听觉感受和心理感知所产生的不同效应。研究中特别引入西方典型弓弦乐器小提琴作为参照系,对其构造和音质特点与中国胡琴乐器之间的同与异进行了相应的比较研究。
关 键 词: 二胡; 京胡; 板胡; 乐器构造原理; 音色物理成因
一、序 言
在中国传统弓弦乐器中,二胡、京胡和板胡在乐器构造、材质和音质特性等方面体现着明显的个性差异,而这三种胡琴乐器的不同特点正好代表着整个中国传统弓弦乐器(胡琴家族) 和现代乐器改革而新生的弓弦乐器的类型特征。① 因此本文以这三种乐器作为典型和“样本”进行研究,以期从中更深入地认识中国整个弓弦乐器构造和音质特征的基本原理。
国际上音乐人类学的研究已经证实,人对音乐的感受一方面与人的先天听觉感受有关,另一方面也与受后天生活环境和文化传统的影响而“习得”的音乐感知和音乐认知有关。② 的确,这种后天的文化传统习得,不仅影响着我们对音乐的感知和认知,而且还不断固化着我们对音乐的生理感受和心理感觉。这就是为什么像吉他、二胡这类发生频率与人嗓发声频率近似的乐器,往往会给人以悦耳感和述说感的原因。但是,由于人类听觉系统在生理机制方面存在着共性特征,因而乐器声音的物理特性也会不时地把人们带回到先天的听觉感受中。这也是为什么乐器的高音部分往往会让人产生紧张、激情等感受,中低音部分往往会让人产生轻松、舒缓的感觉等现象的原因。除了音高之外,不同乐器的音色更能对人的听觉直感和心理感受产生强烈反应。比如: 低音沉重而缺乏高频泛音的音色会给人以忧郁沉重的感觉; 高频泛音丰富的音色则给人明亮轻快的感觉; 高频突出而缺少中、低频段的音色会给人尖锐、响亮但缺少温和的感受。此外,由乐器频率、振幅、音质所形成的声波能量,不仅通过人耳还通过人体的振动和压强对人产生直接的心理影响,如: 通常认为人耳分辨不出 20 赫兹以下低频段的声音,但这种被叫作“次声”的振动波可以和人体器官产生强烈的共振作用。在教堂聆听大型管风琴演奏时,会感觉到莫名的震撼和安抚感,那是因为当音强达到一定程度时,人的内脏由于共振作用会对人产生异常的心理知觉,这也是次声音效作用于人耳和人体所引发听觉感受的基本原理。这就是说,尽管人的后天习得使人的听觉感受具有很强的主观性,但是,乐器声音的客观音响( 音色是这种音响的重要因素) ,对人的音乐听感同样会产生重要作用。正因为如此,分析和研究这三种胡琴类乐器声音的物理成因,不仅能让我们从物理原理方面了解这类乐器音色的构成机理,还有助于我们了解乐器音色的产生机制,进而使我们认识乐器音色作用于人的听觉感应和心理感知的客观的声学原理。
二、三种胡琴形制的共性与个性差异
中国弓弦乐器家族中,二胡、京胡、板胡虽然形制与类型有很大差异,但它们的基本结构却比较相近。它们在构造和发声方面的共同特征是: 都有琴杆、琴轴、琴弦、千斤、琴筒、琴码,另有琴弓( 包括弓杆和弓毛) ; 演奏时,以弓毛摩擦琴弦使其振动而发声( 这时琴弦振动的音量微小) ,通过琴码将弦的振动传给琴筒,经过琴筒的共鸣对声音加以调制,从而发出乐器特有的声音。这三种乐器尽管存在着基本的共同构造和发声原理,但细节方面它们之间存在很多差异。就琴筒而言,二胡的琴筒一般用乌木、紫檀木、红木( 偶有花梨木或竹子) 等密度较大、质地均匀的材料制作,形状六角形最为常见,一般长 13 厘米,前对边口径 8. 8 厘米,筒腰略细,前筒口蒙蟒皮,后筒口敞口或镶嵌雕木花窗形音窗; 京胡,琴筒用毛竹制成,琴筒长 11. 4 厘米、后口直径 4. 3 厘米,前口蒙蛇皮或其他新型膜材料,后敞口; 而板胡的琴筒,也被叫作瓢,通常用椰壳制成,略成截顶半球形,面板用薄桐木板,后敞开或开呈金钱眼状 5 个音孔。二胡的琴杆全长 81 厘米,直径约为 1. 8 厘米,尚选红木,多由乌木制成,也有用檀木,还要尽量选择质地紧密、木射线细密而均匀、无节、无疤,无明显裂痕的材料; 京胡根据用处不同,琴杆长度也略有不同,多用紫竹、白竹、龟背竹或染竹制成,通常有 5 节,1 至 4 节长度一般在 37 ~ 43 厘米之间,上方两节各装有一弦轴,底节插入琴筒中,在筒里的一段杆上,开有长方形、前后对穿的风口; 板胡琴杆全长 70 ~ 73 厘米,一般用小叶檀、乌木、黑檀、老红木等硬质材料制作。二胡的琴码多用木松节码或枫木码; 京胡的琴码由老竹子刻制而成,分空心码和马蹄码两种,而且有大小之分; 板胡的琴码往往用硬木或竹子做成。
二胡较常用的是线绕千斤,所用的有棉线、丝线、有机玻璃、塑料等; 京胡则使用的是黄铜或不锈钢做的 S 形千斤钩,直径在 1. 2 ~ 1. 5毫米,宽度一般在 20 毫米左右; ③ 板胡的千斤又称腰马,使用牛角或红木制成的扁形木片。
当代二胡、京胡和板胡的弦通常选用金属弦(传统的丝弦在20世纪五六十年代逐渐被金属琴弦替代)和马尾弓。
这三种胡琴乐器,由于其构造部件、制作材质和内部结构形态的差异,造成其音色的差异也很大。相比之下,欧洲乐器自文艺复兴时期起走上了一条标准化、结构优化的道路,很多欧洲传统的弓弦乐器逐渐消失或被标准化,专业音乐领域所用弓弦乐器只剩下极具代表性的提琴家族,其中尤以小提琴的音响性能和表现力的优化最为典型。小提琴无论从结构到形状都比本文涉及的这三种胡琴乐器复杂得多。小提琴由包括 4 根琴弦在内的 30 多个零件构成,虽然它也具有和中国胡琴类弓弦乐器相类似的构成部件,如琴头、琴颈、琴 身( 琴 箱) 、弦 轴、琴 弦、琴 马、琴 弓等,但由于小提琴的共鸣箱由具有弧度的面板、背板和侧板黏合而成,致使其声音共鸣得到极大的优化,声音在音箱内的反射和衍射得以合理处置,从而产生更为协和的音质。
小提琴在音箱材质方面也有巧妙配置: 面板常用质地较软的云杉木制作,背板和侧板用质地较硬的枫木,琴头、琴颈用整条枫木,指板用乌木。多种不同质地的木材料的复合结构,也是成就小提琴柔美、明亮音色特性的重要因素。
以上任何一种乐器的发声,都是由乐器部件摩擦而形成振动波,在产生和传导中会通过乐器具体形状、结构、材质对声音产生调制,从而形成一定的谐振效果,即形成乐器特有的音色。本文接下来将通过乐器构造描述及其物理声学公式的解释,对三种胡琴的结构和发音机制进行分析,使用相关物理原理,来解释和分析各种乐器音色产生的物理机制。
三、胡琴的构型与部件对其声学特性的影响
声音是由物体振动产生的波,并通过介质传播被人或动物听觉器官所感知的波动现象。在乐器上,通过特定部件振动而产生的最初的声源波,经过乐器特有的结构进行调制,从而产生( 每种乐器) 特有的谐波,形成音色。由于不同种类的乐器,其几何构型、构件材料,各部位受力情况等存在差异,因而声波产生和传导过程产生的谐波就形成差异,从而产生不同的音色。根据波振动传播的“惠更斯原理”( Huygens principle) ④ ,即波阵面上的每个点都可以看作是一个次级波的子波源,子波的波速和频率等于主波的波速和频率。简单地说,就是介质中每一波动状态是由各处的波动决定的。这样我们就可以用一些有代表性的点的波动状况,来说明乐器的部分特征。乐器的每个部分有自己特定振动的模式和频率,这些频率是乐器所固有的,并不随外界的刺激而改变。物理系统在特定频率下较之其他频率可以以更大的振幅做振动,这种现象被称之为“共振现象”,这些特定的频率与体系的固有频率有关。乐器的固有频率是其音色的一个基本成因。另外,由乐器固有特点造成的波传导过程中的衍射和干涉也会对乐器的音色产生影响。
(一) 琴弦的演变驻波及高频声音
二胡、京胡、板胡都是用琴弓上的弓毛摩擦琴弦,引起琴弦振 动 而 产 生“声 源”波的。虽然这种单靠琴弦振动而产生的声音音量很小,但它却是这类乐器发声的基础。
琴弦的振动再通过琴体结构进行调制,不仅会放大“声源”的音 量,同 时 也 产 生 特 定 的谐波,形成特定的音色。琴弦振动的基本方程为:
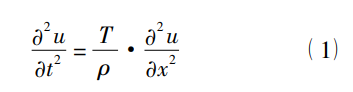
其中 u = u( x,t) ,为在 t 时刻 x 点的振幅,T 为弦上的拉力,ρ 为琴弦的线密度。弦的振动在其两侧固定点的位移恒等于零,这要求在琴弦上可自由移动的部分形成驻波,即弦长需要为波长的整数倍。驻波不仅仅出现在琴弦上,琴的各处都存在特定频率的驻波,如琴的蒙皮、面板、共鸣箱内部空腔、共鸣箱体、琴杆,甚至千斤和千斤之上到转轴的弦上也会出现驻波,可以和驻波产生共振的声音将会被加强,反之则会被消减。对乐器发声影响最大的是蒙皮或面板和共鸣箱内部空腔。由于驻波的存在,琴的任一结构都对琴上的振动进行了筛选和调制,从而产生特有的音色。琴弦达到振动平衡时允许出现的频率是要满足一定数学条件的。其振动频率为:
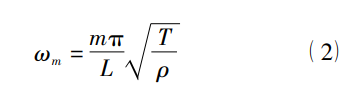
其中 m 是振动的级数,L 是琴弦的长度,同等条件下,考虑单一因素的影响,长度越长的琴弦频率越低,张力越大频率越高,琴弦密度越低频率越高。
根据振动的叠加原理,在基音之外琴弦上还可以出现很多满足驻波条件的波。琴弦会与空气摩擦产生衰减,对于频率高的振动,也就是级数更高的驻波,其单位时间内振动次数也多,与空气摩擦损耗的能量更高,所以更容易发生衰减。从琴弦材质来看,金属弦和丝弦相比较,后者与空气摩擦阻力更大,所以丝弦发出的声音由于缺乏更高频的谐波,显得不如金属弦明亮。同时由于丝弦很难如金属弦一样做得质地均匀,因此会出现非理想状况的非均匀振动,从而造成更高的噪音水平。正是因为以上原因,现代弓弦乐器基本上都使用了金属弦,然而丝弦的某些声音效果是金属弦无法取代的。对于同种弦,产生相同频率和响度的振动,高张力弦的振幅可以更小,受到的空气阻力也相对小,所以高张力弦可以更长时间地保持更高频率的泛音声音,故此显得音色更加明亮通透。
( 二) 干涉现象对乐器声音的影响
干涉是波传播的最主要特征之一,也是乐器实现自身音频选择的一个重要途径。一般机械波的物理表达式为:
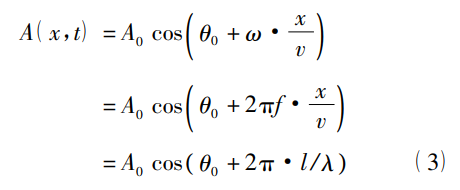
其中: A0 是波的振幅,振幅与其响度相关; θ0 是波的初始相位,这在波的传播过程中十分重要,因为它直接影响着传播过程中的波的干涉和衍射效果,不具备稳定初始相位的波不能产生相互干涉; ω、f 分别为波的角速度和频率,他们满足 ω = 2π·f,对应着音调,在不同介质中传播,频率不变; v 是声音在介质中传播的速度,它和介质的密度、弹性性能有关,在均匀的介质中波的传播速度和方向都不会不变; λ 为声音在介质中的波长,它与频率和声速之间的关系为:
v = λ·f ( 4)
机械波在有相同频率和固定相位时会产生干涉现象,干涉现象有助于增强或消除特定频率的声音。设有两个频率相同的波,振幅分别为 A1、A2,初始相位分别为 θ1、θ2,则它们在某一点产生的振动效果为:
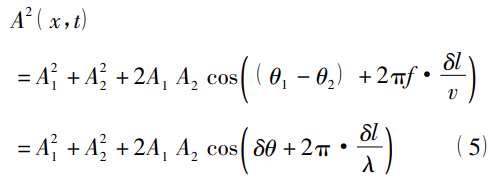
其中(θ1-θ2)为一个固定值,δl 为两束波到达同一点所经过的路程的长度差,我们定义 2π· δlλ = 2πf· δlv ,为在特定介质中声波传递的声程差,当声波发生弹性反射时相位会发生 π 的改变或不变,具体情况与声音发生反射的界面两侧的性质有关,但对于特定路径,声程依然为一个固定值; 而遇到杂质、不均匀界面、非弹性连接等条件的时候会发生非弹性散射,非弹性散射会破坏波的相位,从而无法产生稳定的声程,也就无法产生干涉,反而会因为声音的漫反射和衍射产生很多我们不期望的声音元素,这个原理也可以解释内部出现裂纹的打击乐器会产生鬼音的现象。在此过程中会产生一定的能量损失,这部分能量会作用在非弹性散射点上,对造成非弹性散射的因素产生破坏作用,这正是乐器使用前期声音效果不稳定,经过一段使用,即“开音”后声音变得稳定的原因。该过程会发生在乐器的任何部位,因为在演奏过程中,乐器是处于整体振动中。

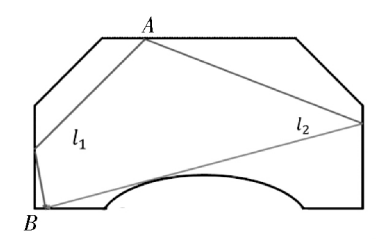
图 1 琴码的示意图。琴弦与琴码的接触点为 A,在 B 点处产生干涉的示意图
本文中所涉及的二胡、京胡和板胡,都是通过琴码将振动传递给琴身上的蒙皮( 或板胡的木板) ,琴弦与琴码接触点可以看作是振动的源点,通过琴码各个点传递给蒙皮( 或面板) 的时候,产生了不同的初始相位差,再作为新的振源在蒙皮( 面板) 上传播。如图 1 所示,A 点为琴弦与琴码的接触点,B 点为琴码与蒙皮( 面板) 接触点,由于声音从不同路径经过反射达到 B 点,图中给出两条路径,经过的长度分别为 l1、l2,于是会产生相位差,当δθ - 2π·l1 - l2λ = ( 2n + 1) π,( n = 0,± 1,±2,…) 时,将出现干涉减弱作用,当然实际情况我们需要对所有可能路径进行求和。一般软木中 声 速 为 3354 米/秒,硬 木 的 声 速 为4267 米/秒,其在琴码的传播时间差远高于人的分辨能力,但是由于传播声速的不同,会产生完全不同的干涉效果。由公式( 2) 可得在声音为 440 赫兹时,软木中声音的波长为7. 62 米,硬木中声音的波长为 9. 70 米,这远大于琴码的大小,也就是在低音区、中音区码子本身波的干涉产生的效果可以忽略,但对于 10000 赫兹以上的高频声波,其波长在厘米范围内,传播过程会由于干涉效果产生明显的滤波效果,同等条件下,软木内同频率的声波波长更长,因此软木琴码产生的声音更为柔和; 在同种材质的情况下,琴码越大,对波长越长即频率越低的声音产生的干涉影响越大,因此使用小琴码的乐器的声音比较透,而使用大琴码的声音则比较闷。同时,软木内部往往呈现蜂窝状结构,相对硬木来说对高频振动的传导能力会差一些。本文将在下面讨论琴皮膜时对类似的现象做进一步的讨论。
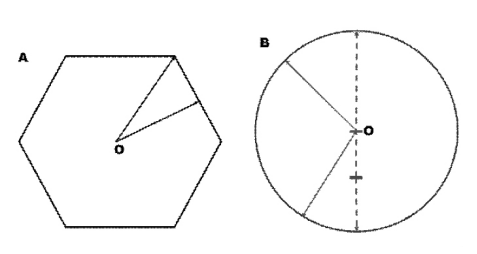
图 2 A 为六角形二胡蒙皮示意图,B 为京胡蒙皮及板胡面板示意图。O 点为其几何中心
同样的振动干涉造成对特定频率的声音消除也会出现在蒙皮( 或面板) 上。图 2 为二胡、京胡琴筒的蒙皮和板胡琴筒的面板示意图。其中,京胡和板胡的琴筒截面是具有很好对称性的圆形,其蒙皮或面板亦呈圆形。
由图 2B 实线可见,如果琴码在中心位置,则声波缺乏声程差,产生不了对特定频率的消音效果,因此在实际使用中很少将琴码放在蒙皮或面板的几何中心,而是偏离中心,于是可以产生一定的声程差,对特定频率的振动产生滤波效果。常见二胡的音筒截面及蒙皮表面呈六角形,这种形状本身就可以制造一定的声程差,如图 2A 所示,当采用更多边的正多边形时,蒙皮上的不同路径的声程差逐渐趋近于圆形,这样通过干涉抑止噪声逐渐趋向对更高频起作用,因此实际使用过程中,二胡共鸣箱往往会采用六角形或八角形。以上三种乐器相较,二胡声音中噪音成分相较另外两种胡琴低,但相对于小提琴,这些胡琴都具有很高的噪音度。小提琴采用了更复杂的几何结构,从而更好地通过干涉作用抑制了噪声的产生。
(三) 不同蒙皮及面板材料对琴声的影响
一般来说,二胡琴筒上蒙的是蟒皮; 京胡琴筒上蒙的是蛇皮; 板胡琴箱上的面板是木板。这些不同的蒙皮或面板材料,是构成其音色差异最主要的因素之一。因为蒙皮或面板的作用,都是把通过琴码传过来的振动进行调制,并通过共鸣箱将音量放大、美化,因而蒙皮和面板的材质值得加以分析和研究。
由于二胡和京胡的蒙皮都与琴筒以一定力相连,琴筒的振动也会影响到琴膜的振动,而板胡的面板虽然是镶嵌入琴筒( 琴箱) 的,但琴筒的振动依然会影响到琴板的振动。如果要对这一现象建立模型,如图 4,这与一些讨论机械结构共振问题所用的模型类似。⑤
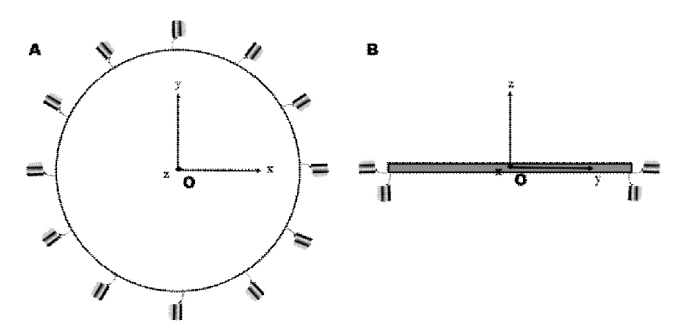
图 3 左图 A 为我们所用模型的顶视图,右图 B 为我们所用模型的侧视图。
密度为 ρ 的膜位于 x - y 平面内,x - y 平面内弹簧提供一个稳定张力 T( 当考虑有刚度薄板时,T 可以认为是薄板的抗弯刚度) ,z 方向的弹簧除了提供膜的张力之外,还提供一个等同于箱体振动的频率 ω存在有固有频率外力作用时,膜等于胁迫振动,最终膜的频率等于策动频率,随着时间的增加,膜和面板会受到外力策动,因而随着时间的经过而无限增大,就会表现出共振现象。因此,蒙皮和面板都可以看作是琴筒上声波频率的放大器。同时,蒙皮和面板又有其固有频率,会对特定频率的声音进行筛选放大。但是一般的实体,其蒙皮、面板具有的特征频率取决于几何结构、材料特性的约束,通常有无数个特征频率,很难得到准确的数学表达解析,这里我们只能作以定性的讨论。设对应的膜或面板的振动方程为 u = u
( x,y) 。对于膜的振动方程为:
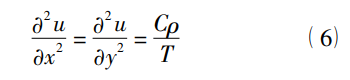
其中,C 为一个常数,ρ 为单位面积上膜的质量,即面密度,T 为膜上的张力,它的固有角频率为:
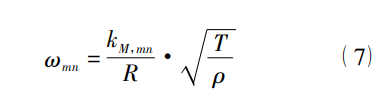
其中 kM,mn 为一个有振动阶数确定的常数,R 为圆形膜的半径。对于板的振动方程形式更为复杂,其自由振动形式下的方程为:
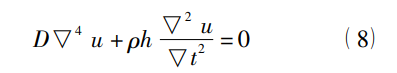
其固有角频率为:
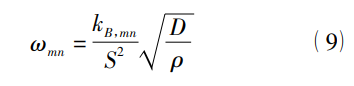
其中 kB,mn 为振动阶数所确定的常数,S
为面板面积,D 为抗弯刚度,它与板材的表示抗拉伸形变的杨氏模量 E,受外力时轴向与横向形变比即泊松比 ν,以及板的厚度 h 的关系为 D = Eh312( 1-ν2)。由于 kM,mn与 kB,mn的计算十分困难,我们只能对它进行定性的分析。
对于蒙皮材料的二胡和京胡,其半径越大在相同张力的情况下固有频率越低; 由于蟒皮的密度高于蛇皮,所以在其他条件相同的情况下,蒙蟒皮的二胡声音频率低于蒙蛇皮的京胡。此外,联系上文所说的声音干涉作用,有更大花纹的蟒皮对波长相对较长的低音频率调制整波效果好,同理,蛇皮对高音调制整波效果好。这也从理论上解释了为什么声音高亢的京胡蒙皮的材料通常选择蛇皮而非蟒皮。而对于使用面板材料的板胡,我们可以看到固有角频率与面积的 - 2 次方成正比。
众所周知,平方的数值增长速度远高于一次方,就是说在其他条件不变的情况下,面积越大,固有频率降低的速度越快,这也可以解释为何中音提琴只比小提琴大 1 /7,但是发出声音音区却相差很大。在刚度 D 中包含厚度,板材的固有频率与厚度的 3 /2 次方成正比,增加板材的厚度可以提高乐器的共振响应频率,乐器声音会变得更加高亢嘹亮,而采用抗变形能力更强的硬木则也可以达到同样的效果,但是没有增加面板厚度有效,因为固有频率与样式模量的平方根成正比; 而采用密度更高的材料,可以降低乐器的响应频率。虽然振动方程的形式与解并不完全相同,但响应的规律也可以用来说明共鸣箱。二胡具有密度最高、表面积最大的共鸣箱,所以二胡的声音相对京胡和板胡是最低沉的。另外,小提琴面板不规则 S 型音孔口,改变了琴面的振动模式,抑制了某些特殊的、不希望出现的振动模式,也降低了小提琴声音模式的噪音成分。
(四) 共鸣箱的影响
共鸣箱是乐器的重要组成部分,它不仅仅可以将声音放大,对声音也会产生一定的调制作用。由于开有音窗,破坏了反射回去的声波的相位,所以可以认为三种琴都属于一端封闭,一端开口状态。下图描述了一端封闭和两端都封闭的腔体中声波形成驻波的情况:
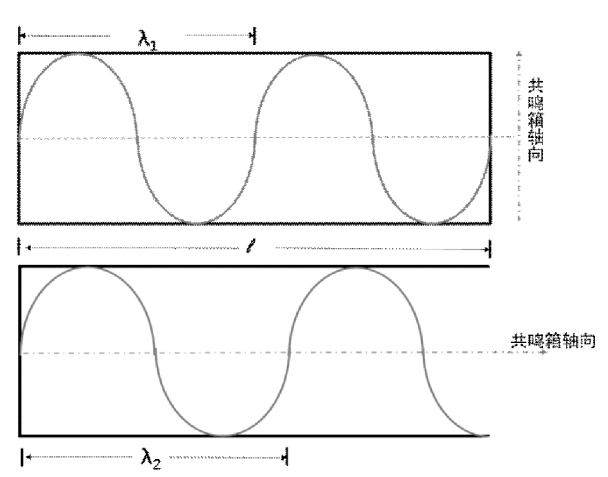
图 4 长度为 l,两端封闭的腔体( 上图) 中驻波的形态,和一端封闭一端开放的腔体中驻波的形态
通过上图可以看到: 对于两端封闭的情况 波 长 λ1 需 要 满 足 l = nλ1,( n = 1,2,3,…) ,此过程发生在与共鸣箱轴垂直的切面方向; 而对于一端封闭一端开口的情况 λ2 需要满足 l = n +12 λ2,( n = 1,2,3,…) ,此过程发生在与共鸣箱轴平行的方向,但当腔体长度远大于波长长度的时候,二者区别就逐渐不明显了。如果取声音在空气中的速度为342 米/秒,这时 440 赫兹的声音所对应的波长为 78 厘米左右,3000 赫兹左右的声音的波长约在 10 厘米左右。我们谈到 的 二 胡、京胡、板胡都有内部结构,可以对切面方向特定频率的声音进行筛选和调制,同时其共鸣箱长度可以对轴向声波进行筛选和调制。三种胡琴乐器的共鸣箱轴向对中高频有较好的调制作用,而对于频率很高的高次谐波的调制、抑制作用则很差,二胡京胡都采用一种截顶圆锥结构,可以对特定音区的声音进行调制;而板胡有些会采用双层结构,产生一个距离比较小的空气夹层,它的存在有助于对高音部分进行调制。二胡和板胡由于有音窗的设计,可以弹性反射回部分声波,形成二次调制乃至多次调制,可以对波长更长的声波进行调制,相对而言可以抑制噪音的频率范围更广; 而京胡由于共鸣箱较短,而且一端完全开口,可以控制的噪音范围相对较小,尤其是高频噪音,这也是京胡音色高亢的一个原因。
而对于小提琴,其共鸣箱厚度和宽度都存在复杂的变化,内部有音梁等设计,造成了复杂的反射效果,从而从共振和音程两方面更好地对噪音进行了抑制,这与共鸣箱结构简单的民族乐器有很大区别。
由于琴杆插入共鸣箱内,会对共鸣箱内声音产生衍射和反射效果。反射对声音的调制作用,在上文“干涉现象对乐器声音的影响”中已经加以解释,这里我们主要讨论衍射的作用。衍射指在声波传播过程中,遇到障碍物或孔洞时,如果声波的波长比障碍物大得多,声波会绕过障碍物而造成传播方向改变。琴杆的尺度和上边结构的尺度往往在厘米量级,对应着 30000Hz 左右的声音,发生衍射后,声波遵循干涉原理,因此合理设计琴杆的插入位置,开口形制可以对高频声音加以调制和抑制。也可以通过在共鸣箱中加入附属结构,利用干涉和衍射对琴的音色进行进一步调整。京胡的琴筒采用了前大后小模式,造成了内壁形成了一个截顶圆锥形状,这样琴膜发出的声波,可以通过反射再次汇聚到琴膜上,这样一方面提升了琴的音量,同时也会对特定波长的声音有调制效果。与以上三种中国典型弓弦乐器相对比,小提琴共鸣箱内部结构复杂,有不同的厚度,从而可以更好地抑制各个频率范围上的噪音。
四、结 论
本文以波动力学为基础,分析了乐器各构成部分固有振动周期的特点,考虑了声波传播过程中的相干效果,分析了典型弓弦乐器二胡、京胡和板胡的音色成因,并与小提琴进行了相应的比较。通过上文的分析和比较研究,得出对这三种胡琴在其构造和物理声学原理方面可能形成的如下一些一般规律和特定音色的调制原则:
1.由于弦振动驻波的存在和空气阻力的原因,弓弦摩擦点更接近琴码可以产生更高频谐音,丝弦的高频谐音没有金属弦丰富,同等情况下高张力弦有更多的高频谐音。
2.声音在乐器上的非弹性传播过程是乐器声音传播的主要动力; 由于不同材质的琴码内部声速的差别,造成的相干效果不同,同等性质琴码,硬质琴码使乐器发声中高频成分更多,同等材质的琴码越小,乐器声音中高音成分越多。
3.二胡的六角形琴膜的不对称性,造成了一定的抑制噪音的效果,为了产生更大的音程差,上述三种乐器演奏过程中,琴码都不会放在膜/板的几何中心。
4.二胡和京胡的蒙皮张力、厚度、面积,以及板胡面板的厚度、面积、抗形变能力等,对乐器的共鸣、音质会产生直接的影响。
5.乐器共鸣箱及其内部结构对弦振声源的传导过程产生了重要的声音调制作用;不同形制和构型材料的乐器共鸣箱( 琴筒)调制出不同的谐音模式,由而产生不同特征的音质(音色)。
以上研究结论,可提供对这三种类型的中国胡琴乐器形制特征、音质特性、音色特点的物理声学认知; 可由此进一步理解这些乐器的这些特征、特性和特点对人的声音听觉感受和心理感知方面产生影响的声学原理;对进一步理性地( 而非单凭感性地) 进行这些民族乐器的改良( 即所谓“乐改”) 也可提供一定的科学参考依据。
致谢: 本文调研、撰写过程中,多次与吉林大学超硬材料国家重点实验室包括教授进行了交流,包括教授在物理声学和乐器材料学方面给予本文直接指导,特此表示感谢。
( 本文系教育部人文社会科学研究一般项目: 中国常用民族乐器音色的声学测定及听觉心理实验,项目编号: 13YJCZH084。)
注释:
① 常见中国弓弦乐器除二胡、京胡、板胡外,还有四胡、坠胡、中胡、高胡、大胡、京二胡以及头弦、二弦等。这类乐器从其名称和来源看,大都可归入传统称谓的“胡琴”类乐器,唯其中广东、福建一带流传的传统乐器头弦、二弦之类不以“胡琴”相称,但从其与唐宋间奚琴相似或相关的历史看( “奚琴”因其出自奚族人而得名。宋 陈 暘《乐 书》有 云: “奚 琴 乃 胡 人 之乐”) ,也不妨将其归入“胡琴家族”。
② 参见 John Blaking: How Musical Is Man? Washington:University of Washington Press,1974.
③ 此处所记乐器部件的尺寸及材料,均依据中华人民共和国工业和信息化部颁布的《中华人民共和国轻工行业标准》( 2011 年版和 2017 版)进行描述。
④ “惠更斯原理”是研究衍射现象的理论基础,可作为求解波传播问题的一种近似方法。该原理由荷 兰 物 理 学 家 克 里 斯 蒂 安 · 惠 更 斯( Christiaan Huygens) 在创立光的波动说时首先提出,故名。
⑤ 参见 1: 李秋红等: 《圆形薄板在任意弹性边界条件下的自由振动》,载《船舶力学》,第 19 卷,2015,第 162 ~ 169 页;参见 2: Wu T Y,Liu Gr. “Free vibration analysisof circular plates with variable thickness bythe generalized differential quadrature rule”[J],Computer Methods in Applied Mechanics and Engineering,2002,191(46) : 5365 ~ 5380.

